C語言以連續的記憶體空間來表達陣列,多維陣列的地址運算採用row major的方式。這種做法的好處是索引運算速度快,甚至能用pointer來逐一檢視其內容。但這種實作方法在傳遞陣列參數時, 就有一些問題產生了
int sum(int x[]) {
// x的長度到底是多少? 不知道的話程式要怎麼寫?
// 如果宣告成 int sum(int x[100])則此函數就只能接受長度為100的陣列
}
int main() {
int x[100];
int y[200];
sum(x);
sum(y);
}
假設有一函數sum(int x[])可用來將陣列內的函數全部加總起來,則僅靠傳遞陣列開頭地址是不夠的,還必須傳遞該陣列的長度才行。如
int sum(int x[], int len) {
int i, total = 0;
for (i = 0; i < len; i++) {
total += x[i];
}
return total;
}
int main() {
int x[100];
int y[200];
sum(x, 100);
sum(y, 200);
}
由於長度的資訊並不在陣列內,必須靠設計者另外告知才行,不小心的話容易發生不一致的情形。
另一種方法是規範該陣列必須以某個特殊的數值當作結尾,函數必須自行檢查該數值,以確保程式正確。C語言的字串就是利用以0結尾的陣列來表達。
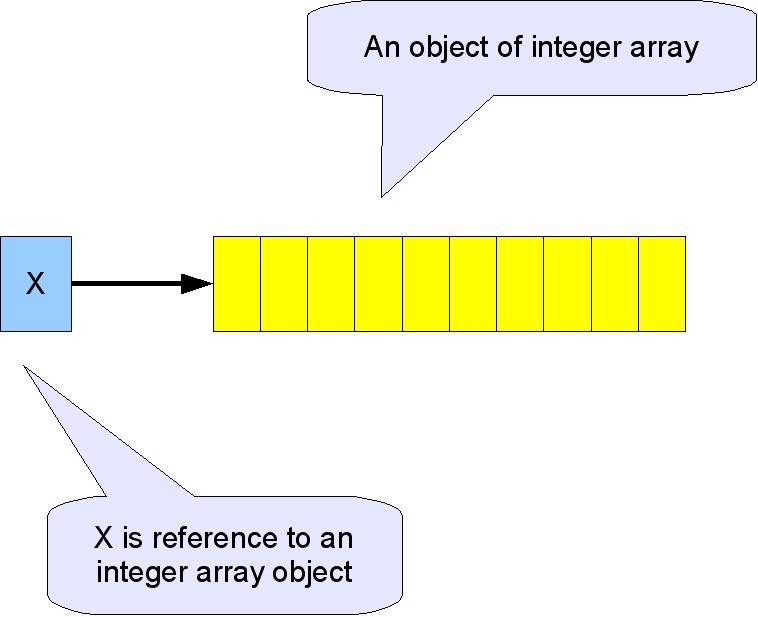
Java的陣列並不以一塊連續的記憶體空間來表達,而是把陣列視為特殊的物件。此物件不但可存放資料,還利用object variable length記錄著該陣列的長度。

public class ArrayExample {
public static void main(String[] argv) {
int[] x; // x is a reference to int[]
x = new int[10]; // 利用new指令產生物件
for (int i = 0; i < x.length; i++) { // 此物件有一個object variable length,用以紀錄該陣列的長度
x[i] = i;
}
}
}
length變數宣告為final,因此陣列物件產生後,就不能再變更其長度了
public class ArrayExample {
public static void main(String[] argv) {
int[] x; // x is a reference to int[]
x = new int[10]; // 利用new指令產生物件
x.length = 1; // Compile Error
}
}
在陣列變數的宣告中,要注意和C語言特別不同的地方是:
我們也可以在變數宣告或是new陣列時就給定初始值:
public class Arrays {
public static void main(String[] args) {
int[] a1 = { 1, 2, 3, 4, 5 };
Object[] a2 = new Object[] {
new Integer(47), new Long(10),
new Float(3.14), new Double(11.11)
};
}
}
public class ArrayExample2 {
public static void main(String[] argv) {
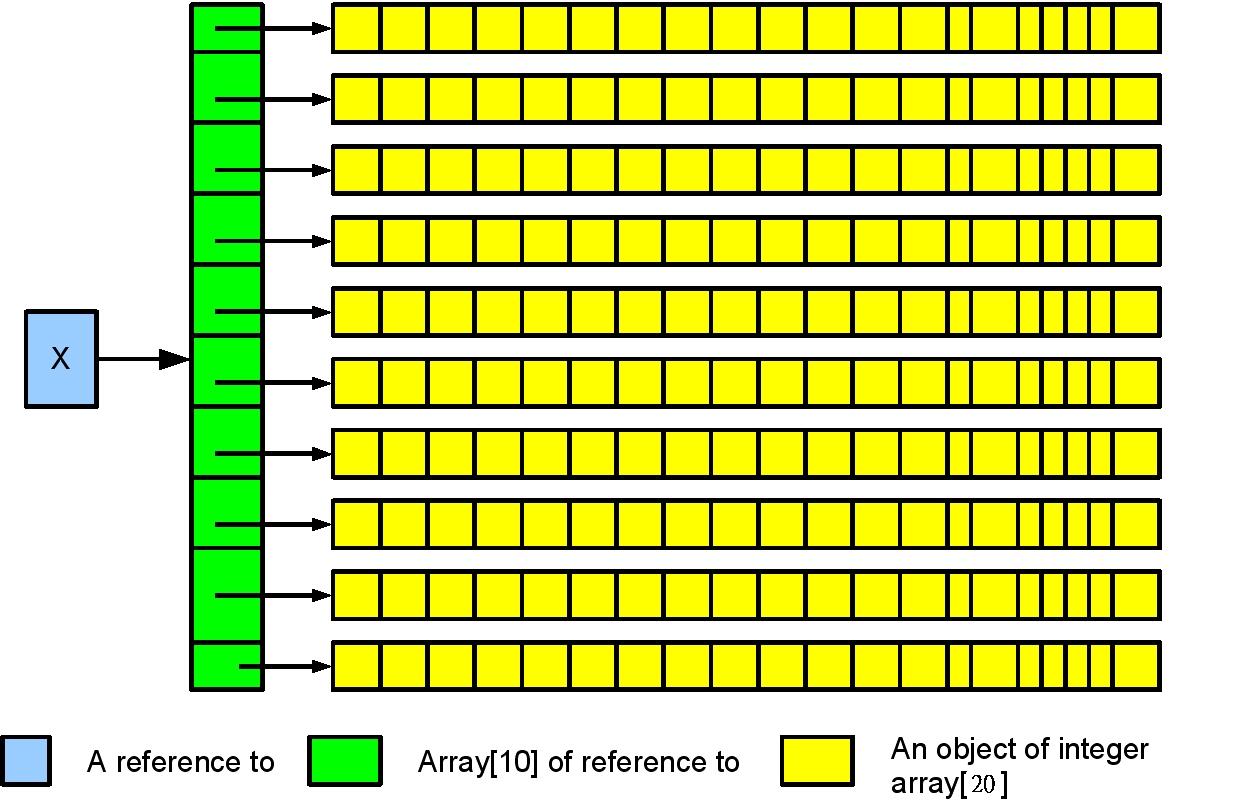
int[][] x;
x = new int[10][20];
for (int i = 0; i < x.length; i++) {
for (int j = 0; j < x[i].length; j++) {
x[i][j] = i + j;
}
}
}
}
上述的範例中,x宣告為reference to int[][],x[i][j]事實上是先找出reference x[i],再找x[i]所指到的陣列物件內的第j個元素。由於Java採用這種機制,因此下面的有趣情形就發生了:
public class ArrayExample3 {
public static void main(String[] argv) {
int[][] x;
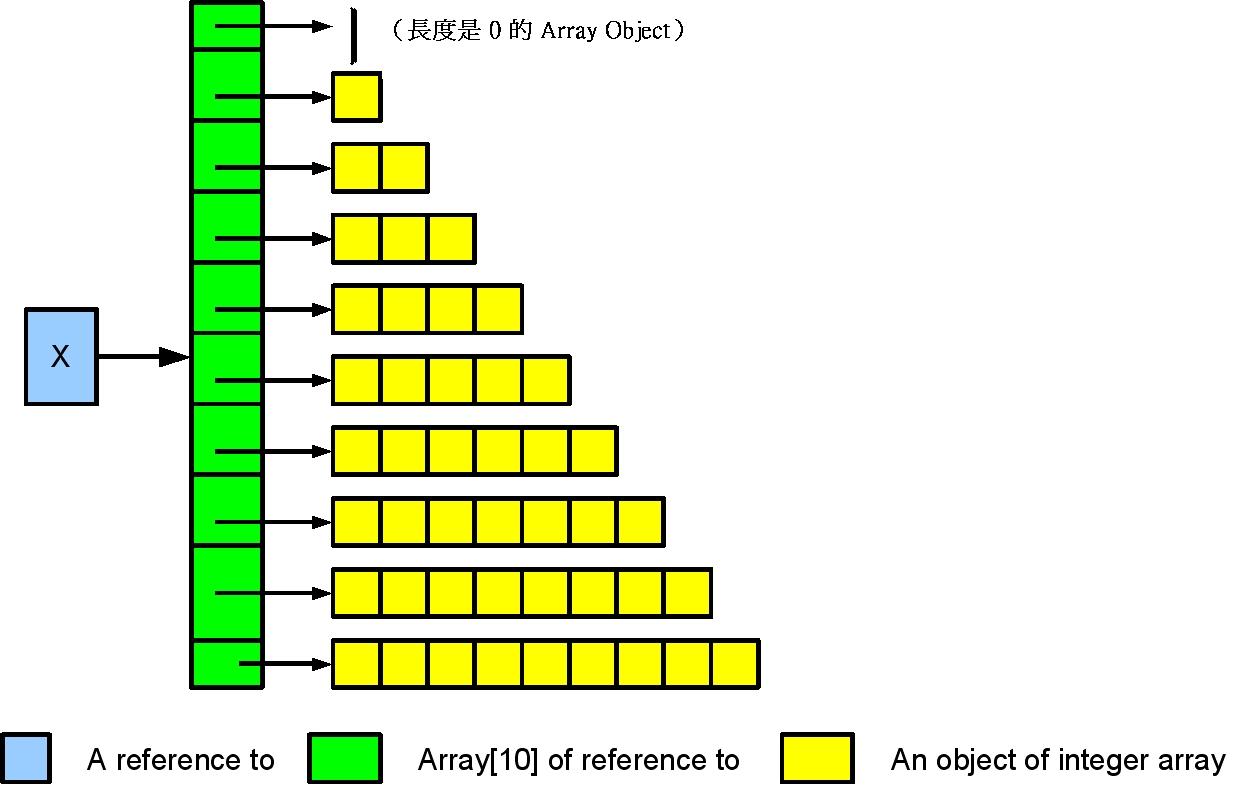
x = new int[10][]; // 先產生x陣列
for (int i = 0; i < x.length; i++) {
x[i] = new int[i]; // 再分別產生x[i]所指到的陣列
}
for (int i = 0; i < x.length; i++) {
for (int j = 0; j < x[i].length; j++) {
x[i][j] = i + j;
}
}
}
}
上述範例有兩點要注意
C語言不會對陣列的索引進行任何檢查,保證索引值在陣列的合法範圍內,是設計者的責任。像是下列的範例就很可能產生Segmentation Fault。
int main() {
int i;
int x[10];
for (i = 0; i <= 10; i++) {
x[i] = i;
}
}
由於這類的疏忽很難完全避免,而且不容易找出錯誤,因此Java在執行期間會對陣列的索引做檢查,如果超出來合法範圍,就會產生ArrayIndexOutOfBoundException的例外。若程式設計時沒有指定這種例外的處理方式,則整個程式會終止,並於螢幕上印出相關的錯誤訊息。例如執行下面的程式:
public class ArrayExample4 {
public static void main(String[] argv) {
int[] x = new int[10];
for (int i = 0; i <= 10; i++) {
x[i] = i;
}
}
}
就會產生如下的錯誤訊息,並且終止該程式
java.lang.ArrayIndexOutOfBoundsException: 10 at ArrayExample4.main(ArrayExample4.java:5) Exception in thread "main"
上面訊息的意義是:
對於寫過C語言的人來說,第一次看到這樣的訊息都會很興奮,因為JVM明明白白的告訴我們哪一行出了甚麼錯誤,要除錯就簡單多了。
當然這樣的便利性是用效能換來的。如果你的應用需要大量存取陣列,而且速度非常重要,連幾個machine cycle都要計較,那才要考慮不用Java了。
public class Fab {
private static long[] rel = {0,1,1,2,3,5,8,13,21,34,55,89};
public static void main(String[] argv) {
val(10);
}
public static long val(int n) {
if (rel.length <= n) {
long[] tt = new long[n+1];
int i;
for (i = 0; i < rel.length; i++) {
tt[i] = rel[i];
}
for (; i <= n; i++) {
tt[i] = tt[i-1] + tt[i-2];
}
rel = tt;
}
return rel[n];
}
}
public class SelectionSort {
public static void main(String[] argv) {
int[] data = {6, 3, 7, 1, 4, 8};
sort(data);
for (int i = 0; i < data.length; i++) {
System.out.println(data[i]);
}
}
public static void sort(int[] data) {
for (int i = 0; i < data.length - 1; i++) {
// find minimun in i ~ data.length - 1
int mim = i;
for (int j = i + 1; j < data.length; j++) {
if (data[min] > data[j]) {
min = j;
}
}
// swap data[i] with data[min]
int tmp = data[i];
data[i] = data[min];
data[min] = tmp;
}
}
}
public class InsertionSort {
public static void main(String[] argv) {
int[] data = {4, 1, 7, 8, 9, 3, 2};
sort(data);
for (int i = 0; i < data.length; i++) {
System.out.println(data[i]);
}
}
public static void sort(int[] data) {
int j, pivot;
// insert data[i] to sorted array 0 ~ i - 1
// begins from i = 1, because if the array has only one element then it must be sorted.
for (int i = 1; i < data.length; i++) {
pivot = data[i];
for (j = i - 1; j >= 0 && data[j] > pivot; j--) {
// shift data[j] larger than pivot to right
data[j+1] = data[j];
}
data[j+1] = pivot;
}
}
}
下圖為n=6的情況
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
其規則是最外層是1, 裡面每個數字都是上方兩個數字的和.
Pascal Triangle是(x + y)n每個項次的係數.
提示: 如果把上圖左邊的空白拿掉則會變成下面的圖形, 除了最左邊和最右邊的數字是1以外, 裡面的每一個數字都是其正上方和左上方數字的和. 你可以用陣列來計算和儲存這些數字, 然後再以上圖的格式印出來.
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1所以只要你能回答下面問題, 程式就寫完了:
以下是程式的範例:
/**
* Program Name: Pascal.java
* Purpose: print pascal triangle on screen
* Author: Shiuh-Sheng Yu, Department of Information Management
* National ChiNan University
* Since: 2006/01/23
*/
public class Pascal {
public static void main(String[] argv) {
int n, i, j;
int[][] tri = new int[51][51];
n = Integer.parseInt(argv[0]);
if (n < 0 || n > 50) {
System.out.println("I can only print Pascal triangle between 0 and 50.\n");
} else {
for (i = 0; i <= n; i++) {
for (j = 0; j <= i; j++) {
System.out.print(" "+(tri[i][j] = (j==0 || j==i) ? 1 : tri[i-1][j-1]+tri[i-1][j]));
}
System.out.println();
}
}
}
}
public class Example {
/* 列出由at左邊所有的排列 */
private static void permutation(int data[], int n, int got) {
// 如果已經排到最後了,印出結果
if (n == got) {
for (int i = 0; i < n; i++) {
System.out.print(data[i]+" ");
}
System.out.println();
return;
}
int tmp;
for (int i = got; i < data.length; i++) {
// swap data[i] and data[at]
tmp = data[i];
data[i] = data[got];
data[got] = tmp;
// 然後遞迴呼叫,以找出got+1右邊的所有排列
permutation(data, n, got + 1);
// swap back data[i] and data[got]
tmp = data[i];
data[i] = data[got];
data[got] = tmp;
}
}
public static void permutation(int data[], int n) {
permutation(data, n, 0);
}
public static void main(String[] argv) {
int data[] = {1,2,3,4,5,6};
permutation(data, 4);
}
}
public class Example {
/* 由data.length取n個 */
private static void combination(int[] data, int n, int got, int from) {
int tmp;
if (n == got) {
for (int i = 0; i < n; i++) {
System.out.print(data[i] + " ");
}
System.out.println();
return;
}
for (int i = from; i < data.length; i++) {
// 選第i個, by swap data[i] and data[got]
tmp = data[i];
data[i] = data[got];
data[got] = tmp;
combination(data, n, got + 1, i + 1);
// swap back data[i] and data[got]
// two swaps make data original
tmp = data[i];
data[i] = data[got];
data[got] = tmp;
}
}
// data裡找出所有n個數字組合
public static void combination(int data[], int n) {
combination(data, n, 0, 0);
}
public static void main(String[] argv) {
int[] data = {1,2,3,4,5};
combination(data, 3);
}
}
public class Example {
public static void main(String[] argv) {
char[] data = {'1', '2', '3', '4'};
reverse(data);
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]+" ");
}
}
public static void reverse(char[] data) {
char tmp;
for (int i = 0, j = data.length - 1; i < j; i++, j--) {
tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
}
}
public class Stack {
private Object[] data;
private int top;
public Stack() { // constructor
data = new Object[1024];
}
public void push(Object obj) {
if (top >= data.length) {
Object[] tmp = new Object[data.length*2];
System.arraycopy(data, 0, tmp, 0, data.length);
data = tmp;
}
data[top++] = obj;
}
public Object pop() {
return data[--top];
}
public Object peek() {
return data[top-1];
}
public int size() {
return top;
}
}