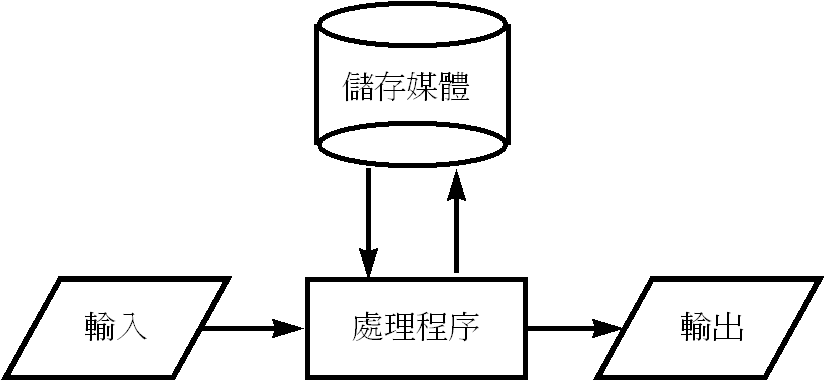
電腦是一種用來處理資訊的機器。我們可以用圖一的"輸入--處理--輸出"的模型來描述電腦系統工作的方式。這個"輸入--處理--輸出"的模型是由電腦硬體、軟體和資料等三個元件所組成。電腦硬體是作為輸出入資料和處理資料的實體媒介。系統軟體和應用軟體則提供了電腦硬體執行指令的確實順序。資料是我們用來表達資訊的媒介,他們以用各種不同的格式存在,並可被電腦系統處理。以規腦硬體和系統軟體組成了電腦系統的架構(Computer System Architecture),以提供使用者在其上執行應用程式和處理資料。

圖一 電腦系統處理程序
一個簡化的典型的電腦系統架構可由圖二來表示。電腦的運算是由中央處理單元(Central Processing Unit, CPU)來執行。它包含了控制單元(Control Unit, CU)和算術邏輯單元(Arithmetic and Logic Unit, ALU)兩大部份。控制單元用來解釋電腦指令,搬移CPU內部資料,以指揮協調CPU各部份的運作。ALU是電腦指令主要的執行部份,它又可細分成加法器、乘法器、及多個暫存器(Register)等部份。暫存器是CPU內部用來儲存資料的地方。
記憶體是用來儲存程式和資料的地方。一般又稱為RAM(Random Access Memory)或Main Memory(主記憶體)。我們可將記憶體視為由一個個小格子所組成的陣列,每個格子內都儲存著一個二進位數字以代表程式指令或資料。我們給每一個格子一個特有的編號,稱為地址(Address),就像我們的門牌號碼一樣,可供CPU定址某一塊記憶體。
輸入輸出(Input / Output, I/O)裝置是我們最常見的硬體元件。常見的輸入元件有鍵盤、滑鼠、搖桿、DVD光碟機(或燒錄機)等。常見的輸出元件有螢幕、印表機、喇叭等。可同時做輸入輸出的元件有磁碟機、磁帶機等儲存媒介及網路卡等。CPU、RAM和之間是由匯流排(Bus)連接起來。Bus係作為連接其上各硬體元件交換電子資料的路徑。
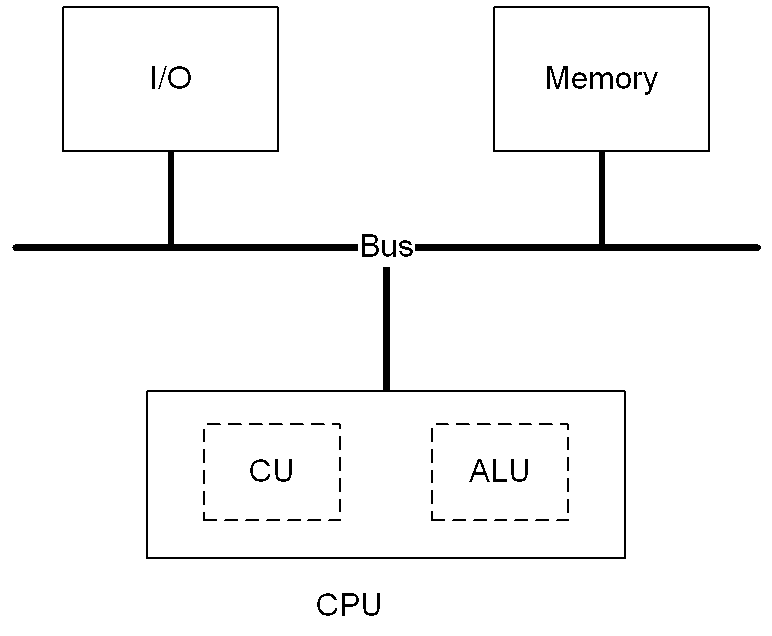
圖二 電腦系統架構
軟體元件是由許多的程式(Program)所組成。這些程式是用來指揮電腦硬體的運作,以達我們的工作。我們一般將軟體分為系統軟體和應用軟體兩大類。系統軟體幫我們管理檔案、分配電腦的各種資源、執行程式以及從鍵盤接收我們的命令。其中和管理電腦相關的一些程式我們稱為作業系統(Operating System),如Window NT和UNIX都是一種作業系統。而應用軟體則幫助我們完成特定的工作,如Word可用來編輯文書,Excel可用來作分析計算等。作業系統是電腦系統不可或缺的一部份,當電腦啟動時,首先會執行儲存在唯讀是記憶體(Read Only Memory, ROM)內的程式,此程式會從本地磁碟機或透過網路從伺服器的磁碟機上將作業系統載入記憶體(Random Access Memory, RAM)內執行,然後我們就可以透過輸入裝置下達命令,以執行應用程式來處理我們的資料。
數字表示法
在十進位系統中, 43 = 4*10 + 3, 而527 = 5*102 + 2*10 + 7。目前的電腦大多使用二進位系統,我們稱一個二進位數字為一個位元(Bit, Binary Digit)。由於bit實在太小了,現在記憶體的最小儲存單位通常為8 bits,又稱為byte。下圖是二進位系統的計數方式:
|
二進位 |
等於 |
十進位 |
|
0 |
0*20 |
0 |
|
1 |
1*20 |
1 |
|
10 |
1*21 + 0*20 |
2 |
|
11 |
1*21 + 1*20 |
3 |
|
100 |
1*22 + 0*21 + 0*20 |
4 |
|
101 |
1*22 + 0*21 + 1*20 |
5 |
|
110 |
1*22 + 1*21 + 0*20 |
6 |
|
111 |
1*22 + 1*21 + 1*20 |
7 |
|
1000 |
1*23 + 0*22 + 0*21 + 0*20 |
8 |
|
1001 |
1*23 + 0*22 + 0*21 + 1*20 |
9 |
|
1010 |
1*23 + 0*22 + 1*21 + 0*20 |
10 |
一般而言,以B為底的K個數字所能表達的範圍為R = BK。以二進位為例,不同的位元數所能表達的數字如下表:
|
位元數 |
表達範圍 |
|
1 |
2 |
|
4 |
16 |
|
8 |
256 |
|
10 |
1,024 |
|
16 |
65,536 |
|
20 |
1,048,576 |
|
32 |
4,294,967,296 |
|
64 |
約等於 1.6*1019 |
|
128 |
約等於 2.6*1038 |
十進位加法表
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
4 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
二進位加法表
|
+ |
0 |
1 |
|
0 |
0 |
1 |
|
1 |
1 |
10 |
八進位加法表
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
|
2 |
2 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
|
3 |
3 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
|
4 |
4 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
|
5 |
5 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
|
6 |
6 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
7 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
十進位與其他數字系統的轉換
137548= ????10
|
(84) |
(83) |
(82) |
(81) |
(80) |
|
|
4096 |
512 |
64 |
8 |
1 |
|
|
X |
1 |
3 |
7 |
5 |
4 |
|
4096 + 1536 + 448 + 40 + 4 = |
|||||
|
612410 |
|||||
612410 = ??????5
612410 = x*5n + ... + a*51 + b*50
將兩邊除以5會得到
1224 餘 4 = x*5n-1 + ... + a*50 餘 b
因此可求得b = 4. 重複此過程可得解如下:
5 ) 6124 ( 4
5 ) 1224 ( 4
5 ) 244 ( 4
5 ) 48 ( 3
5 ) 9 ( 4
5 ) 1 ( 1
0
因此
612410 = 1434445
其他數字系統間的轉換:先轉成十進位再轉成另一個數字系統。
在電腦系統中我們通常以八個Bits為一個單位稱為位元組(Byte)。因為24 = 16,我們通常以兩個十六進位數字來表示一個位元組,因此十六進位系統是除了二進位系統外另一個常用的數字系統。在十六進位系統中我們以ABCDEF來表示10到 15的數字。其加法表和乘法表請自行畫出。二進位和十六進位間很容易轉換, 這是因為16 = 24, 所以每4個一組的2進位數字, 可以直接轉成1個16進位的數字。如11010111011000這個二進位數字我們可以由右至左把他分為11 0101 1101 1000四組,各組數字翻成十六進位就成為35D816 。若要轉成8進位,由於8 = 23因此由右至左每三個一組 011 010 111 011 000 = 327308。
0.122013 = 0.???10試問
==> 0.122013 = 1/3 + 2/9 + 2/27 + 0/81 + 1/243 = 0.33333+0.22222+0.07407 + 0.00412 = 0.6337410
或
(81+2*27+2*9+1)/243 = 0.63374
0.82812510 = 0.???2 0.82812510 = a*2-1 + b*2-2 + c*2-3 ...試問
|
0.828125 * 2
|
|
|
|
|
|
|
0.82812510 = 0.1101012所以
程式可以用任意的格式來儲存和處理資料,這樣的格式我們稱為專屬格式。但為了便於在不同的硬體和軟體平台間交換資料,我們必須用標準的格式來表示資料。標準格式通常是由國際標準組織訂定,或因某類軟體廣為流行而後成為標準。常見的資料型態和標準如下表:
|
資料型態 |
標準 |
|
字元 (character) |
ASCII, EBCDIC, Unicode |
|
影像 (位元應對bit map) |
GIF, JPEG, TIFF, Windows Butmap |
|
影像 (物件) |
PICT, PostScript |
|
向量圖形與字型 |
PostScript, TrueType |
|
聲音 |
Sound Blaster, WAV |
|
視訊 |
MPEG, QuickTime |
ANSI(American National Standards Institute)所制訂的ASCII(American Standard Code for Information Interchange)及IBM所定義EBCDIC(Extended Binary Coded Decimal Interchange Code)是兩種常用的英文文數字元編碼方式。EBCDIC是8 bits的編碼方式(只定義了28=256個字元),目前僅限於IBM的大型主機和終端機使用。ASCII則是7 bits的編碼(只定義了27 = 128個字元,很多程設書的附錄都有表可查),目前廣泛使用於各種電腦和終端機。近年來ISO(International StandardsOrganization)在ASCII的基礎上為不同的語言訂定了不同的8 bits編碼。不過8 bits僅能表示256個字元,對象形字語言是不夠的。因此IOS提出了16 bits的Unicode以取代舊有的7 bits和8 bits字元。Unicode試圖將世界上的主要語言全部納入,在一個編碼空間下表達所有的語言文字。目前Java語言是採用Unicode作為其編碼的方式。Windows也採用Unicode。
常見的字元輸入裝置:鍵盤(keyboard)、光學辨識機(Optical Character Recognition, OCR)、條碼機(bar code reader)、語音輸入、中文手寫辨識、打孔機(punched card)。
不管資料的格式為何,電腦內部都是以不同大小的二進位數字來代表。這些二進位數字的解釋方法是由兩個因素來決定:
CPU所能處理的運算。
用來產生應用程式的程式語言所能提供的資料型態。
如何表示整數資料
有號整數
有一種方法稱為 "符號與大小表示法":第一個
bit作為正負號,其他的bits為大小。缺點是不好運算,因為加法的運算方法和運算元的正負號有關。當兩個運算子同號時,只要將數字大小的部份相加,正負號與運算元相同即可,但當兩個運算子的符號不同時,則要以減法來處理大小的部份,正負號則視相減的結果而定。這種表示法也會造成電腦邏輯線路設計上的困擾。減法比加法難實作的原因是減法需要一直借位, 而加法只要記得前一對數字加起來有沒有進位即可。有人就想出一種數字系統,可以用二進位的加法取代減法,讓邏輯線路設計簡單,跑起來又快的。就是補數系統。
補數(Complement)
我們先以最多兩個數字的10進位數字系統為例。
60-30 = 60 + 70 - 100。
而-100可以藉由 "忽略溢位" 來達成。所謂 "溢位" 是指數字計算的結果超過硬體線路所能表達的範圍,以兩個數字的10進位數字系統為例,只能表達0-99,所以算出來的結果若大於99就發生 "溢位" 。而 "忽略溢位" 在此例中就是指 "丟棄" "忽視" "省略" 第3位數的意思。因此-30就可由+70與 "忽略溢位" 來達成。接下來的問題就是如何由30得到70? 70 = 99 - 30 + 1。讀者此時的疑問是,減法又跑出來了,這樣會比較快嗎?請注意99減任意數都不需要借位,因此線路比較好設計。補數的觀念用到二進位時,效用就更大了。所有都是一的二進位數111111,減去二進位數X,得到Y,此時X和Y每一個對應的bit都是相反的,如1111 - 0101 = 1010。換言之,求二進位的補數可以用bit inverse來取代減法,而bit inverse則是最容易實作的電路。99 - 30稱為30的9補數,99 - 30 + 1稱為30的10補數。
令Y為10進位所能表達的最大數字, 則在9補數中X的負數是以(Y-X)來表達. 例如最多3位數的10進位系統中,300的9補數以(999-300)=699來表達. 因此最多3位數的10進位系統中, 其9補數的對照表如下
500 …999 | 0…499
-499…-000 | 0…499
上表是說999代表-0,998代表-1,997代表-2,...,500代表-499。9補數有兩個0,+0和-0,可表達的範圍在-499 ~ +499。
10補數中X的負數則定義為(Y-X+1), 因此最多3位數的10進位系統中, 其10補數對照表如下:
500 …999 | 0…499
-500…-001 | 0…499
上表是說999代表-1,998代表-2,997代表-3,...,500代表-500。所以10補數能表達的範圍在-500 ~ +499。
9補數減法:將-X的運算, 改為 + (-X), 若有溢位, 則將結果再加1
420-170
=>420+829
=1249 => 249 + 1
100 - 350
=> 100 + 649
= 749
-100-200
=>899+799
=1698 => 698 + 1
10補數減法則不必考慮溢位
Y: 11111111 X: 01110011 Y-X: 10001100因此在二進位的1補數系統中, 不需要用到減法, 只要將X的每一個bit都反過來, 就可得到-X了.
浮點數表示法
本節是為了完整敘述各種數字的表達法而寫的, 讀者若看不懂, 並不會影響對C語言的瞭解, 因此可跳過此節的細節部份。
前面介紹了整數的表達法, 但對許多應用來說(尤其是科學運算), 整數是不夠用的, 必須用到浮點數才行。為甚麼不說是 "實數", 而要說 "浮點數" 呢? 這是因為電腦是 "有限位數的二進位系統", 所以能表達的數字有限, 不但不能表達像π這種無理數, 甚至無法表達1/3這個有理數。而且各種應用所需的數字大小和精準度不同, 有些要表達很大數字(像天文學), 有些要表達很小的數字(像高能物理學), 如何設計一種 "可表達範圍很大且有小數" 的二進位表示法, 就成為一項挑戰。各位還記得科學符號表示法嗎? 2008這個數字的科學符號表示法是2.008E3。E代表指數(Exponential)部份, 所以2.008E3是表示2.008 * 103的意思。因為這種表達法的小數點不會固定放在個位數後面, 而是會依據所要表達的數字大小而 "浮動", 所以才會被稱為是 "浮點數"。我們常用32 bits(C稱為float)或64 bits(C稱為double)來存放浮點數, 其標準由IEEE制定。它表達的是這種形式的科學符號:
+0.01E10 表示 (1+1/4)*22。老師你寫錯了吧, 應該是(1/4)*22吧? 這是因為二進位系統中只有0和1兩個數字, 因此正規化後的科學符號表示法的整數部份一定是1, 換句話說任何數字都長這個樣子, ±1.mmmmEee, 既然整數一定是1, 那就不要浪費了, 以便可以表達更大範圍的數字。上述例子的±稱為(Sign bit), ee部份稱為Exponential(指數), mmmm稱為Mantissa(尾數), 以下的SEM就是這幾個字的縮寫。
一個
IEEE(Institude of Electric and Electronic Engineering, 電子電機工程協會, 是一個全球最大的學術組織) 32位元的浮點數以下面的格式來表示:SEM
S占1bit為正負號,E占8bits為指數部份,M占23bits為尾數部份。其中指數部份採用excess-127表示法,即範圍為-127~128,但0和255有特殊意義,所以實際範圍為-126 ~ +127其中
|
指數部份 |
小數部份 |
所代表的值 |
|
0 |
+-0 |
0 |
|
0 |
非 0 |
+-2-126*0.M |
|
1 ~ 254 |
任何值 |
+-2E-127*1.M |
|
255 |
+-0 |
+-infinite |
|
255 |
非 0 |
特殊狀況(NaN) |
IEEE 64位元浮點數表示法
SEM
其中S占1bit為正負號,E占11bits為指數部份,M占52bits為尾數部份。
其中指數部份採用excess-1023,表示範圍超過10 + -300次方