在程式語言教學中，訓練學習者分析問題的能力相當重要。很多有趣的範例程式來自數學家
的研究，以八皇后為例，Franz Nauck在1850年提出「在西洋棋的棋盤上放八個皇后，使得
沒有一個王后能吃掉其他皇后」。西洋棋的皇后如同象棋的車，可以縱、橫、斜向移動，把
8個皇后排在8乘以8的棋盤上，卻不使彼此攻伐的排法有幾種？數學家高斯猜測有96個解，
實際上只有92個形式解，本質解有12個。本質解是無法經由某一個解旋轉或反射得到的解。


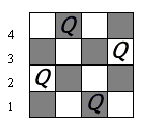
八皇后問題可以擴展成N皇后，藉由程式語言的幫助將易於求解。在教學上為了方便解說，
以四皇后說明此類問題的核心想法。使用四維向量(a,b,c,d)表示四皇后在4乘以4棋盤上的
放法，圖一的擺法表示成(2,4,1,3)。



    

    
圖一
圖二


假使如圖二，已排好三個皇后，對應的向量為(1,4,2,X)，第四個分量X是未確定的第四個皇
后位置。N皇后求解的條件是：沒有任兩個皇后在同一行、同一列、同一對角線上。圖二的(
1,4,2,X)不管怎麼放，都不可能符合上開條件。下列樹狀圖每個節點表示棋盤上放皇后的一
種情形，詳細說明所有可能的排法。

 
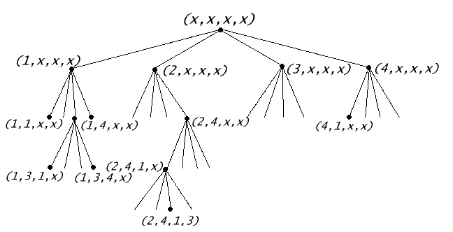
由樹狀圖看來，找出四皇后問題的解，最好的辦法是檢查所有的狀況一次，此次有44=256個
可能解，不僅耗費時間，問題擴大時也難以負荷。改用一個比較可行的方法來處理，首先，
依次序先檢查(1,X,X,X)，再往下層檢查(1,1,X,X)。因為(1,1,X,X)表示前兩個皇后都位於
第一行上，違反條件。所以(1,1,X,X)以下的子樹的樹枝就都不必再逐一的搜索了。這時，
應退回到上一級的頂點(1,X,X,X)處，以下一個頂點(1,2,X,X)開始。可以發現(1,2,X,X)這
個頂點也違反了條件，因為同一對角線上。於是再返回(1,X,X,X)。現在利用圖四至圖七，
以此方法繼續做下去：


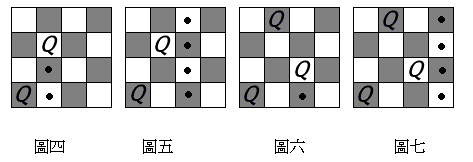
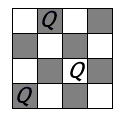
圖四，表示第一個皇后放在第一行，第二個皇后就不能放在第一列也不能放在第二列，只能
以第三列開始搜尋；
圖五，表示以(1，3，×，×)為樹根的子樹都不是問題的解，因為第三個皇后無論怎麼放，
都違反條件；
圖六，表示(1，4，1，×)違反條件，而(1，4，2，×)仍能符合條件；
圖七，表示(1，4，2，×)在考慮第四個皇后位置，就被否決了。
    
按上述方式做下去，可得到一個結論：四皇后問題共有兩個解，如圖八中的(2,4,1,3)和圖
九(3,1,4,2)。

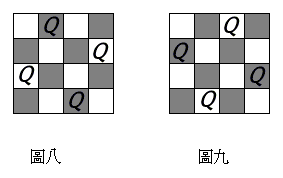
讓我們審視(2,4,1,3)和(3,1,4,2)這兩個解，發現它們是互相對稱的，本質上是同一個解，
在這裡，我們得到了數學上形式解和本質解的觀念。以上是N皇后問題的解說，以程式語言
求解的範例如下：

範例：N皇后問題
/**
 * Program Name: Queen.java
 * Purpose: 找N皇后問題有幾組解
 * Author: Shiuh-Sheng Yu
 * Date: 2003/05/20
 */
import java.io.*;
public class Queen {
    private int[] board, directions;
    private int size, numSolutions;
    public static final int QUEEN = 0x01000000;
    public static void main(String[] argv) {
        int size, c;
        for (;;) {
            StringBuffer sb = new StringBuffer();
            System.out.print("Please input the Queen size: ");
            for (;;) {
                try {
                    c = System.in.read();
                    if (!(c>='0' && c<='9')) {
                         if (sb.length()>0) break;
                         continue;
                    }
                } catch(IOException ex) {
                    return;
                }
                sb.append((char)c);
            }
            try {
                size = Integer.parseInt(sb.toString());
            } catch(NumberFormatException ex) {
                continue;
            }
            if (size==0) break;
            Queen x = new Queen(size);
            x.arrange();
            System.out.println("The "+size+" Queen has "+x.getSolutionNum()+" solutions");
        }
    }
    public Queen(int size) {
        this.size = size;
        directions = new int[3];
        directions[0] = size+1; 
        directions[1] = size+2; 
        directions[2] = size+3;
        board = new int[(size+2)*(size+2)];
        int lastLine = (size+2)*(size+1);
        // 設定盤面上的哨兵
        for (int i=0; i< size+2; i++) { // 上下兩排
            board[i] = -1;
            board[lastLine+i] = -1;
        }
        for (int i=1; i<=size; i++) { // 左右兩排
            board[i*(size+2)] = -1;
            board[i*(size+2)+size+1] = -1;
        }
    }
    public int getSolutionNum() {
        return numSolutions;
    }
    public void arrange() {
        arrange(1);
    }
    /**
     * 嘗試放到第row列
     */
    private void arrange(int row) {
        for (int i=1; i <= size; i++) { // 檢查此列上的每一行
            int puton = (size+2)*row+i;
            if (board[puton] == 0) { // 不在任何皇后範圍內
                if (row==size) { // 已經到最後一個row, 此為一種解
                    numSolutions++;
                } else {
                    board[puton] = QUEEN; // 放上皇后
                    for (int j=0; j<3; j++) { // 設定此皇后的勢力範圍
                        for (int k=puton+directions[j]; board[k]>=0; k+=directions[j]) {
                            board[k]++;
                        }
                    }
                    arrange(row+1);
                    board[puton] = 0; // 移除皇后
                    for (int j=0; j<3; j++) { // 移除此皇后的勢力範圍
                        for (int k=puton+directions[j]; board[k]>=0; k+=directions[j]) { 
                            board[k]--;
                        }
                    }
                }
            }
        }
    }
}